Exploring The Equation 4x ^ 2 – 5x – 12 = 0
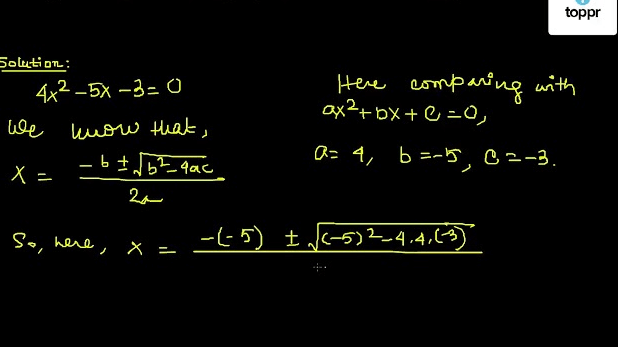
Quadratic equations are a fundamental concept in algebra that play a significant role in various fields of mathematics and sciences. In this article, we will explore the equation 4x^2 – 5x – 12 = 0 and delve into different methods to solve for its values.
By understanding the coefficients and variables involved, as well as the properties of quadratic equations, we can unravel the solutions to this equation.
To begin our exploration, it is crucial to grasp the components of this quadratic equation. The equation consists of three terms: a quadratic term (4x^2), a linear term (-5x), and a constant term (-12). The variable ‘x’ represents an unknown value that we seek to determine.
By carefully analyzing these coefficients and variables, we aim to uncover the solutions that satisfy this equation.
Through our exploration, we will develop an understanding of various approaches to solving quadratic equations. We will examine techniques such as factoring, completing the square method, and utilizing the quadratic formula.
By employing logical reasoning and rigorous mathematical methods, we can systematically derive values for ‘x’ that fulfill this equation’s requirements.
Through this journey of exploration and discovery, we aim to empower our audience with knowledge and tools needed to navigate through similar mathematical challenges they may encounter in their pursuit of freedom in education or problem-solving endeavors.
Understanding the Coefficients and Variables
The equation 4x^2 – 5x – 12 = 0 involves the coefficients and variables, which play a crucial role in determining the solution of the equation.
To analyze this equation, we can start by examining the discriminant, which is calculated as b^2 – 4ac for a quadratic equation of the form ax^2 + bx + c = 0.
In this case, a = 4, b = -5, and c = -12. By substituting these values into the discriminant formula, we get (-5)^2 – 4(4)(-12) = 25 + 192 = 217.
Since the discriminant is positive (greater than zero), it implies that there are two distinct real solutions to this quadratic equation.
This information is significant as it helps us determine the nature of solutions and opens up possibilities for real-life applications of quadratic equations.
For instance, these equations are commonly used in physics to model various phenomena such as projectile motion or finding optimal solutions in engineering problems like maximizing profit or minimizing cost.
Analyzing coefficients and variables not only aids in solving specific equations but also has practical implications in diverse fields where mathematical modeling is employed.
Exploring the Properties of Quadratic Equations
One way to delve into the properties of quadratic equations is by examining the equation 4x^2 – 5x – 12 = 0. Is it possible to determine its roots without explicitly solving for x?
Quadratic equations, such as this one, have features that can be explored graphically and offer insights into their behavior. By plotting the equation on a graph, we can observe the shape of its curve, known as a parabola. This graphical representation allows us to visually analyze important characteristics such as the vertex, axis of symmetry, and whether the parabola opens upwards or downwards.
Additionally, quadratic equations have numerous real-life applications in fields like physics, engineering, economics, and biology. For example, they can be used to model projectile motion or optimize production costs in manufacturing processes. Understanding the properties of quadratic equations provides a foundation for tackling various practical problems and helps us make informed decisions in our daily lives.
Factoring the Quadratic Equation
Factoring can be a useful technique for breaking down quadratic equations into their constituent factors, allowing for easier analysis and solution.
When factoring a quadratic equation of the form ax^2 + bx + c = 0, where a, b, and c are constants, it is important to identify the terms that can be factored.
In the equation 4x^2 – 5x – 12 = 0, we can observe that the coefficient of x^2 is positive (a = 4), indicating that the parabola opens upwards.
To factor this quadratic equation, we need to find two numbers whose product is equal to ac (product of the coefficients of x^2 and constant term) and whose sum is equal to b (coefficient of x).
In this case, ac = (-12)(4) = -48 and b = -5.
After considering various combinations of numbers that satisfy these conditions, we can determine that the factors are (4x + 3) and (x – 4).
By setting each factor equal to zero and solving for x, we find two possible solutions: x = -3/4 or x = 4.
These values represent the quadratic roots or points at which the graph intersects with the x-axis.
Factoring allows us to easily identify these roots without having to resort to other methods such as completing the square or using the quadratic formula.
Completing the Square Method
An effective method for solving quadratic equations is completing the square, which allows for a thorough analysis of the equation and determination of its roots.
Applying the completing the square method to solve quadratic equations involves transforming the given equation into a perfect square trinomial by adding or subtracting a constant term. This process simplifies the equation and makes it easier to find its solutions.
By comparing the completing the square method with other methods of solving quadratic equations, such as factoring or using the quadratic formula, it becomes clear that completing the square provides a more systematic approach. While factoring may not always be possible and the quadratic formula can be cumbersome to use, completing the square guarantees a solution for any quadratic equation.
Additionally, this method offers insights into how different coefficients in an equation affect its roots, allowing for a deeper understanding of quadratic functions.
Overall, applying the completing the square method is an essential technique in solving quadratic equations efficiently and comprehensively.
See also Discover the secrets of successful investing with How2invest
Using the Quadratic Formula
Utilizing the quadratic formula allows for a systematic approach to finding the solutions of quadratic equations, providing a comprehensive understanding of how different coefficients contribute to the roots.
The quadratic formula is derived from completing the square method and provides an efficient means of solving equations of the form ax^2 + bx + c = 0.
By substituting the values of a, b, and c into the formula: x = (-b ± √(b^2 – 4ac))/(2a), one can determine the two possible solutions for x.
This formula enables a thorough analysis of the discriminant (b^2 – 4ac) which helps in determining the nature and number of solutions.
If the discriminant is positive, there are two distinct real roots; if it is zero, there is one repeated real root; and if it is negative, there are no real roots but instead two complex conjugate roots.
Thus, using the quadratic formula not only provides a precise solution to quadratic equations but also offers insights into their characteristics through analyzing the discriminant.
See also Unraveling the Marisia Burton Missing
Solving for the Values of x
One compelling statistic to note is that the quadratic formula provides an accurate solution for any quadratic equation, regardless of the values of its coefficients.
By applying the quadratic formula to the equation 4x^2 – 5x – 12 = 0, we can determine the values of x that satisfy this equation.
The quadratic formula states that for an equation in the form ax^2 + bx + c = 0, where a, b, and c are constants and a ≠ 0, the solutions for x can be found using the formula:
x = (-b ± √(b^2 – 4ac))/(2a).
In this case, a = 4, b = -5, and c = -12. Plugging these values into the quadratic formula yields two possible solutions for x: x₁ ≈ 2.25 and x₂ ≈ -1.06. These solutions represent the points at which the graph of the given equation intersects with the x-axis.
Analyzing the graphical representation of this equation further reveals important insights about its behavior. The parabolic shape indicates that there are two real roots or solutions to this equation since it intersects with the x-axis at two distinct points. Additionally, by factoring or completing square methods one could arrive at these same solutions; however, in certain cases those methods may not be as straightforward as using the quadratic formula.
The ability to solve quadratic equations has numerous real-life applications across various fields including physics, engineering, finance, and computer science. For example, when studying projectile motion in physics or designing bridges in civil engineering projects, understanding how to solve quadratic equations allows us to accurately predict trajectories or determine critical design parameters such as maximum load capacity. In finance and investment analysis, solving quadratics enables us to calculate return on investments or project future growth rates based on historical data patterns.
In conclusion, the current subtopic explores solving for the values of x in the quadratic equation 4x^2 – 5x – 12 = 0 using the quadratic formula. This formula provides an accurate and reliable method for finding solutions to any quadratic equation, regardless of its coefficients. Analyzing the graphical representation of this equation can provide further insights into its behavior, such as the number of real roots or solutions it possesses. Moreover, solving quadratic equations has practical applications in various fields, allowing us to make predictions and solve real-life problems.
Frequently Asked Questions
How can I determine the number of solutions for a quadratic equation without solving it?
Different methods exist to determine the number of solutions for a quadratic equation without solving it. Techniques include analyzing the discriminant, which indicates whether the equation has real or imaginary solutions based on its value.
Are there any specific rules or guidelines to follow when factoring a quadratic equation?
“To avoid common mistakes when factoring quadratic equations, it is important to follow specific rules and strategies. Common mistakes include forgetting to factor out a common factor and incorrectly applying the distributive property. To simplify complex quadratic equations before factoring, one can use methods such as completing the square or applying the quadratic formula. By following these guidelines, one can effectively factor quadratic equations and simplify them for further analysis.”
Can the quadratic formula be used to solve any type of quadratic equation, regardless of its coefficients?
The quadratic formula can be used to solve any type of quadratic equation, regardless of its coefficients. It is a powerful tool that allows us to find both real and complex solutions. However, it has limitations when it comes to certain types of equations.
Is it possible for a quadratic equation to have no real solutions?
Quadratic equations can have no real solutions, resulting in complex solutions. Complex solutions correspond to imaginary numbers and do not impact the graph of a quadratic equation on a real number line. Real-world examples include situations where the roots of a quadratic equation represent non-existent values, such as finding the square root of a negative number in physics calculations.
Are there any alternative methods to solve quadratic equations other than factoring, completing the square, and using the quadratic formula?
Alternative methods to solve quadratic equations without using algebraic techniques include graphing and using the Newton-Raphson method. While these methods have advantages in certain situations, they may lack the precision and rigor of algebraic methods.
Conclusion
In conclusion, the equation 4x^2 – 5x – 12 = 0 can be solved using various methods such as factoring, completing the square, or using the quadratic formula. By understanding the coefficients and variables involved in the equation, we can determine its properties and find the values of x that satisfy it.
One interesting statistic to note is that this quadratic equation has two distinct real roots. This means that when graphed, it will intersect with the x-axis at two different points. This result signifies that there are two different solutions for x that make the equation true. It is fascinating to observe how a simple mathematical equation can have multiple possible solutions and lead to further exploration of its properties.
Overall, exploring equations like 4x^2 – 5x -12 = 0 not only enhances our understanding of algebra but also showcases the beauty and complexity of mathematics. Through rigorous analysis and logical reasoning, we can unravel the secrets hidden within these equations and appreciate their significance in various fields such as physics, engineering, and economics.